Laplace

Las funciones de transferencia con las que se trabaja en el curso están en función de s. ¿Qué significa “s”? s es la variable compleja de la frecuencia.

Pero en la vida real se trabaja con funciones de variable real (generalmente tiempo o distancia). La transformada de Laplace reemplaza estas variables reales (tiempo) por variables complejas (frecuencia). En el dominio del tiempo las expresiones suelen ser complicadas, con exponentes e integrales, que son muy engorrosas de manejar. Entonces la transformada de Laplace convierte estas funciones en función del tiempo (t) a funciones en función de la frecuencia (s). Las expresiones resultantes son muchísimo más sencillas de utilizar. La técnica de transformada de Laplace ahorra cálculos y da una visión mucho más clara de los conceptos.

Laplace también resulta muy útil a la hora de formar las funciones de transferencia, ya que relaciona el sistema físico eléctrico con una expresión matemática.

Para dar un ejemplo de cómo se transforma un circuito eléctrico a una función de transferencia en función de s sólo hay que conocer unas pocas equivalencias:

Un condensador se representa como 1/Cs, una bobina se representa por Ls y una resistencia, al no variar con la frecuencia queda constante R.

La forma de ir formando la impedancia total del sistema es exactamente la misma como si todos los componentes fueran resistencias, pero tomando sus equivalencias en s.

Así, dos elementos en serie se suman: Z=Z1+Z2

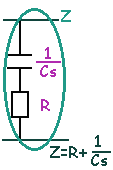
Y dos elementos en paralelo siguen la forma:

Y de esta manera se van construyendo las funciones de transferencia.

En los sistemas funcionales las letras mayúsculas se utilizan en la entrada y salida de los sistemas y las funciones de transferencia representan transformadas de Laplace de cantidades que son funciones de la variable compleja s. Las funciones de s generalmente se abrevian con una letra mayúscula que aparece sola. Las funciones de frecuencia nunca se abrevian.

Como definición de Laplace se suele dar:

“Sea f(t) una función real de una variable real t definida para t>0. Entonces,

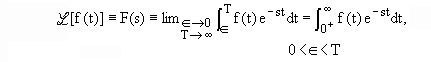
es lo que se llama la transformada de Laplace de f(t).”

s es una variable compleja definida por

donde es la parte real de una variable compleja s, y se suele escribir como Re(s) y w también es una variable que al ir acompañada por j es la parte imaginaria de s: Im(s).

Se ha incluido una tabla de antitransformadas, es decir para pasar del dominio de la variable compleja (s) a la variable real (t). Así se podrán dar los resultados en función del tiempo.